Challenging Periods Reimagined: Road to dynamic challenging periods

[daniFi]

Check out the new Three Sigma’s article, the first of a two-part series, about a novel approach to reduce and optimize Optimistic Rollup’s challenging periods.
Below, me and @3s_drep_fi provide a brief introduction to this article.

Preface

Ethereum’s scalability challenge is a significant obstacle to its widespread adoption, which Layer-2 scaling solutions, like optimistic rollups, aim to address. Optimistic rollups aggregate transactions in batches off-chain, which are then submitted to Ethereum’s mainnet. However, this solution comes with its own set of challenges, such as the length of the challenging period and the use of a centralized sequencer. The length of the challenging period affects the security and efficiency of the system, while the choice between a centralized and decentralized sequencer impacts its reliability and control.
Solutions currently employ a 7-day challenging period, but no solid justification has been found for this value. It’s important to ask whether it makes sense that all types of transactions have the same challenging period. In fact, there may be a need to reduce the period according to transaction risk and sequencer history, while improving the user experience and maintaining security. This includes transitioning to a decentralized network of sequencers without, ideally, increasing L2 costs.
The first topic is introduced here.

Rationale for the Dynamic Challenging Period Model

The current 7-day challenging period is considered too long and expensive for a malicious sequencer to block the L1 network with invalid transaction batches. To prevent this, a challenging period should be set such that it is not profitable for a malicious sequencer to conduct a denial-of-service (DoS) attack on the network. Sequencer reputation and the aggregated value of the batch should be considered when determining the challenging period. A minimum challenging period should also be enforced to prevent invalid small-value transactions.
Furthermore, the challenging period of a given batch must end at the same time or after the previous batch to ensure that finalized batches imply the finality of previous batches. This condition is applied after a batch time is computed, as follows:
T_B = max { CP_min , G_T x min { 7 days , T ( S_TotalCost = V_B ) } }
where:
CP_min: The minimum challenging period required to submit a fraud proof for a given batch;
T ( S_TotalCost = V_B ): Function that gives the amount of time required for a malicious sequencer spend the same amount of value in a DoS attack that they could potentially earn from the aggregated value of the corresponding batch (V_B).
G_T: Governance-adjusted time factor (between a minimum threshold and 1), based on sequencer’s reputation, which will be addressed in a Part II of the series.
On top of this, the aforementioned condition of previous batches being finalized first must be applied. To gain a full understanding, refer to the corresponding section of the article.

Minimum Challenging Period

The discussion of how short the challenging period can be has already been brought up in 2020. Ethereum’s consensus mechanism was still Proof-of-Work, with a minimum of 4.5 hours being derived, assuming a 15-second block time. However, there were consensus failures lasting more than that. The minimum challenging period must not be shorter than this time range. If it were, a malicious sequencer could take advantage of the network’s instability and increase the likelihood of successfully submitting fraudulent batches in the mainnet.
For the current model, one of the first consensus failures in Ethereum’s blockchain, which lasted around 21 hours until its resolution, is considered. To determine the minimum challenging period, it was assumed that the probability of a malicious sequencer leading a successful DoS attack on the L1 network would decrease exponentially as the number of submitted blocks increases:
P_sucessfull-DoS-attack = exp ( - A1 x N_blocks )
If the attack is to be successful in just one block, then one may consider that as a quasi-certain attack:
P_sucessfull-DoS-attack = 99% => A1 = 0.001. Contrarily, if one assumes that an unlikely attack has: P_sucessfull-DoS-attack = 0.1%, then the attempt of attack has to be sustained for 6908 blocks. Given a 12-second block time, the equivalent time period is 23 hours.
Considering it exceeds the 21-hour consensus failure resolution described, the minimum challenging period in the present model will be:
CP_min = 23h
For more information on the results, please refer to section “Minimum Challenging Period” of our report.

Understanding the time for equalizing batch value with cost of spamming L1 network

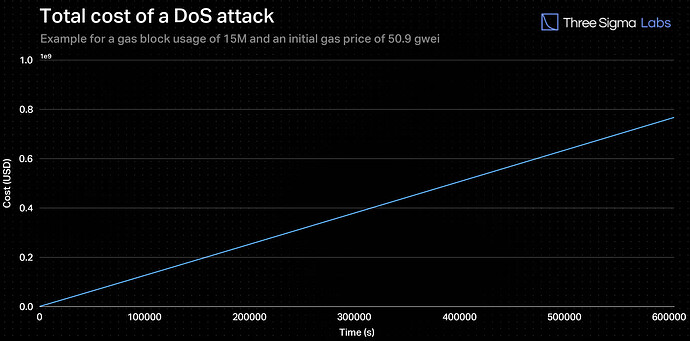
The goal of this section is to explain how to find the time required for a malicious sequencer to spend the same amount as possible earnings from an invalid batch during a DoS attack on Ethereum’s mainnet. The malicious sequencer submits transactions that are prioritized at the top of the block and consume all available gas to prevent other honest L1 network transactions (including fraud proofs) from being included in the blockchain. This creates an adversarial environment where gas prices increase as the malicious sequencer tries to outbid other traders in the mempool. Over time, fewer agents are willing to pay high fees, leading to less competition and a decrease in the rate of escalation of gas prices. Therefore, the evolution of gas prices, thus the transaction cost, over a large time scale, is considered to be logarithmic.
By integrating the transaction cost evolution function over time in a DoS attack, a total cost function was derived. This function represents the cost that a malicious sequencer would incur to spam the network for an increasing number of blocks. The function is given below:
S_TotalCost = ( t + 10^{-2} ) x 7.2222 x ln( t + 10^{-2} ) - t x [ 7.2222 x ( 1 + ln( 10^{-2} ) - GasPrice x GasUsed ] + GasPrice x GasUsed - 7.2222 x 10^{-2} x ln( 10^{-2} )
where GasPrice is the price of gas at t = 0, and GasUsed is the gas usage of a block, which may be considered equal to 15 million.
Each time a batch is being submitted, the current gas price is obtained from an oracle and, by utilizing this function, the equation S_TotalCost = V_B is solved and the corresponding value of T is computed. For example, with a initial gas price of 50.9 Gwei and block gas usage of 15 million (regular limit), a batch with an aggregated value of 400 million USD will have a T of 88 hours.

For more information on the results, please refer to section “Understanding the time required for equalizing batch value with the cost of spamming L1 network” of our report.

Summary

Part I introduces the concept of the challenging period in optimistic rollups, during which users can dispute incorrect transactions. The length of this period affects system security and efficiency. The proposed dynamic model reduces the period based on transaction risk (and sequencer honesty, in Part II), improving user experience without compromising security. Potential attack vectors are addressed and a minimum challenging period of 23h is recommended. Lastly, the model estimates the time required to balance batch value with the cost of spamming the L1 network during a DoS attack by a malicious sequencer.
Check out the Twitter discussion at https://twitter.com/threesigma_xyz/status/1635676314609889282.

Next-up

Next week, Part II will be released. The following topics will be addressed:

• Governance-adjusted time factor G_T;
• Decentralized Sequencer Network, based on a novel selection process;
• New economic incentive to attract sequencers and push them to be honest;
• Notes on malicious behaviour penalization and on how eigenlayer novel approach can be included.

[edfelten]

The main censorship concern that forces the current seven-day challenge period involves L1 block builders who deliberately fork the L1 chain to suppress any blocks containing transactions they want to censor.

If the adversary controls enough block-building share, they can do this for as long as they want, and only a social response from the Ethereum community can stop the attack–as things stand now.

Any proposal to reduce the challenge time should address the forking censorship attack.

[daniFi]

Dear @edfelten,

We invite you to read the full Part I (and, when released, full Part II) of our “Challenging Period Reimagined” series. Here is the link:

Road to a Dynamic Challenging Period

One of our references was your article from 2020, in which you proposed reducing the challenging period to 4.5 hours. We believe this is a real issue that can be optimized, and thus we have proposed a novel model.

We do not disagree with the fundamental idea that you have stated, as we referenced your latest article in our post. However, forking censorship attacks are a problem that affects L1 as a whole, assuming a dishonest majority of agents acting. This impacts not only batches coming from L2 but also every transaction directly related to L1, and thus would affect the overall security of L1. Therefore, we do not believe it is the major topic to focus on. In reality, the most probable scenario is malicious behavior from sequencers rather than block builders in L1. That is why we have designed our model to be economically irrational for a sequencer to act dishonestly in a network of decentralized sequencers, as proposed in Part II.

Nevertheless, the solution you have proposed for the forking censorship problem is very interesting and is not mutually exclusive with our proposal. In fact, we believe they can complement each other.

Kind regards,
@daniFi and @3s_drep_fi

[edfelten]

In a practical system, I don’t think it’s possible to ignore a feasible attack, just because others can be attacked in the same way. An approach is needed that can resist forking censorship attacks, because those could possibly happen on the real chain.

(You also seem to have a model of the sequencer’s role that differs from Arbitrum. In Arbitrum the sequencer only determines the ordering of transactions. No harm is done if the sequencer includes an invalid transaction–the chain will correctly determine that such a transaction should be discarded. The sequencer will end up paying for the L1 gas to include that transaction, which hurts the sequencer but no one else.)

[daniFi]

Dear @edfelten

As Arbitrum works towards a more decentralized paradigm with the emission of a new token, as you highlighted on your Twitter account, we are also proposing a mechanism to decentralize the sequencer (as you’ll see in Part II), while striving to solve the ultimate problem of optimistic rollups: the long challenging periods.

The decentralized sequencer model we are discussing has similarities with the block builder/validator of the L1 mainnet, which has been proven to work. Here, a sequencer bundles L2 transactions into a batch, orders them, and then submits them to L1.

You claim that the sequencer only orders transactions, but in fact, there is always some agent (in Arbitrum’s case, centralized) that submits batches to L1. If the submitted batch has invalid transactions, only L1 users who are verifying the validity of the state can attest to security. The sequencer can then attack the L1 network through a DoS, which is a real threat. With our model, this is not economically rational.

(apologies for the deleted post)

Kind regards,
@daniFi and @3s_drep_fi

[edfelten]

If the submitted batch has invalid transactions, only L1 users who are verifying the validity of the state can attest to security.

Can you explain what the above statement means? I don’t think it’s an accurate description of how Arbitrum works. In Arbitrum the sequencer does not claim that the transactions in its batches are valid, nor does it make any claim about what state would result from executing those transactions. Its only role is to record the byte strings that are submitted to the L2 mempool, and attest to the order in which they were submitted.

As a courtesy, the sequencer can discard transactions that it thinks are invalid. But this is not required and the rest of the protocol does not assume that the sequencer has done it.

You may be thinking of validators, which play a different role in the protocol. There are already multiple validators, and again the protocol does not assume that any particular validator is honest.

[3s_drep_fi]

Dear @edfelten,

We think it is just a question of nomenclature. In our model a sequencer is equal to an Arbitrum sequencer + Arbitrum validator. So, in practice, it all leads to the same outcome and same problems. When we formulated our model, we tried to generalize to any L2 optimistic rollup, not specifically Arbitrum.

Imagine the following scenario: Arbitrum’s sequencer and validator are colluding, inserting invalid transactions in the batch. The Validator submits the RBlock in L1 and then initiates a DoS attack to spam the L1 netowrk, therefore not allowing anyone to submit fraud proofs.
What is your solution for this?

You could say that 7 days is too expensive to do this and this is true. On the other hand, this is completely not optimized, degrading the UX in L2, namely in terms of L1 withdrawals.
Moreover, why should the challenging period be the same for every RBlock submitted to L1?

These are the important questions that need to be answered and it is exactly that we focused in our article. With our solution, with economically rational agents, you will safely shorten Challenging periods.

Kind regards,
3s_drep_fi and @daniFi

PS:

There are already multiple validators, and again the protocol does not assume that any particular validator is honest.

This is not true. You will need at least one honest active validator, as it is stated in Arbitrum glossary.

[edfelten]

I’m not sure I understand your threat model. If someone tries to keep all of the blocks of the L1 network full, the L1 basefee will increase exponentially, and the attack will become prohibitively expensive. For example, if the L1 basefee is 20 gwei when the attack starts, after 20 minutes of completely-full L1 blocks, the cost to fill the next block will be about $60 million. After an hour, the cost to fill the next block will be about $1 sextillion. So that attack is not a concern, compared to attacks that try to subvert the L1 consensus process.

In particular, L1 forking censorship attacks seem like a much more serious threat.

[3s_drep_fi]

Dear @edfelten,

In our article, we thoroughly discuss with clear justifications and research that exponential evolution does not occur like that. First, as you see here (Ethereum Network Utilization Chart | Etherscan), the blocks are already full at 15 million gas (50% Gas limit), and there is no escalation because block builders choose not to do so.

Therefore, if exponential evolution were to occur, it would be short-lived, and block builders would quickly fill blocks of only 15 million to maximize their rewards and encourage transaction participation, as higher fees would be too expensive for users. So, in reality, the DoS attack will be done with blocks filled around 15 million, because that is where the economic competition really is.

Even so, our model for the cost of a DoS attack represents a conservative estimate and is only one of several factors we have considered. Being a conservative approach which already allows shorter challenging periods is a clear improvement to the current status quo and that should not be disregarded as a possible solution.
While we acknowledge that there is always room for improvement, we are not trying to disregard any potential solutions. Rather, we hope to provide a better understanding of the issues at hand. We kindly suggest that you read and reflect upon this question as many of your inquiries may already be answered here (or in Part II, which will be released on Tuesday).

Regarding the “feasibility” of attacks:
First, as you said, “In a practical system, I don’t think it’s possible to ignore a feasible attack,” as ours is. Regarding probabilities, isn’t the attack you mentioned highly unlikely? Do you really believe that having a dishonest majority of validators in L1 capable of forking the blockchain is a stronger issue than having one single malicious sequencer (or Arbitrum Validator+Sequencer, in your protocol) submitting invalid batches and spamming L1 network (as long as it is profitable)? If so, why is that attack not being performed already for other levels of L1?

To clarify, we want to emphasize that we are not attempting to overshadow your solution or your considerations. In fact, it’s possible that our proposal could complement yours. However, it’s not responsible to undervalue this threat and disregard the possibility of reducing the challenging period in this way, especially since it doesn’t exclude the potential for a censorship oracle smart contract to exist.

Kind regards,
3s_drep_fi and @daniFi

[edfelten]

@3s_drep_fi

Therefore, if exponential evolution were to occur, it would be short-lived, and block builders would quickly fill blocks of only 15 million to maximize their rewards and encourage transaction participation, as higher fees would be too expensive for users. So, in reality, the DoS attack will be done with blocks filled around 15 million, because that is where the economic competition really is.

The behavior you describe (builders refusing to fill blocks above 15M gas) is not what is observed in practice; it is not the behavior that was assumed in designing Ethereum’s gas mechanism; and it does not align with the incentives of block builders.

A builder making a block has incentive to include transactions up to 30M gas, as long as there are more transactions that are willing to pay the current basefee and offer a non-minimal priority fee. By including such a transaction, the block proposer gets the transaction’s priority fee. There is no disadvantage to the current block proposer (who is the one deciding whether to include the transaction) of including it.

[daniFi]

Dear @edfelten,

We think that you are not seeing the thing properly and we will elucidate you (a careful read of both our articles would clarify this but we have the courtesy to explain here).

It is not a matter of whether the block builder fills the block with 15M of gas due to its own intention or not. The way the base fee mechanism works basically forces gas usage in each block to oscillate between 15M and 30M. The increase of the base fee makes users not want to send their transactions and spend a lot, thus participation reduces. Block proposers will in fact receive less fees because of that. Of course, the malicious sequencer could try to send 30M transactions regardless but that does not align with his goals.

The exact way the evolution of gas usage per block varies and, therefore, the transaction cost varies in this circunstance, is quite difficult to model.

Therefore, as our part I explains, we model the evolution of the transaction costs in a DoS attack depending on a GasUsage of the attacking transactions. It can be whatever. We exemplifiy the model with the blocks filled at 15M (minorant) as well as with 30M (majorant).

If the implementation is used assuming a 15M gas usage, then it is conservative, which increases the soundness and security of our model, because, in fact, at some points the malicious sequencer performing a L1 DoS attack must send transactions with more than 15M of gas.

We would also want to state that we cannot talk about everything in detailed here in the forum post since our investigation was profound and detailed - we did not just throw numbers out of the sky. Therefore, only a careful and dedicated read of the whole series will enlight about this particular block gas usage topic as well as the remaining of the subjects in our model.

Kind regards,
daniFi and @3s_drep_fi

[edfelten]

In practice, roughly half of Ethereum blocks use more than 15M gas, and a significant fraction use the full 30M gas. Here’s a histogram of Ethereum basefee change (block-to-block) from August 2021-November 2022. These map directly to gas consumption.

[3s_drep_fi]

Dear @edfelten,

1. We kindly ask you to clarify the meaning of the x-axis and y-axis (base fee change? what is that, and in what units) in that histogram. It is not clear.

2. May you provide the source of that data or graph?

3. According to Etherscan, a platform with the information of every block on the blockchain, the Average gas used per block / Block Gas limit (30M) is around 50% (ie. 15M), as you can see in the image below (August 2021 - March 2023), or here: Ethereum Network Utilization Chart | Etherscan.
   Therefore, we do not understand your statements.
   

   

Best regards,
3s_drep_fi and @daniFi

[edfelten]

You claim that every ethereum block has 15M gas or less. But your evidence shows only that the average over many blocks is 15M.

If you want to know whether Ethereum has any blocks above 15M gas, the best approach is to look at actual Ethereum blocks. What you’ll see is that such blocks are common.

Here is the actual distribution of recent block sizes currently reported by Etherscan. As you can see, many blocks use more than 15M gas, and a significant number use 30M gas.

[Edit, to clarify the graph. The x-axis is Ethereum block number. Y axis is gas. Each vertical blue bar represents the gas usage of one Ethereum block.]

[3s_drep_fi]

@edfelten

Thank you for sharing a graph in your previous reply and then not answer to any question regarding it or even explaining it.

You claim that every ethereum block has 15M gas or less

• I am starting to doubt that you read any of our answers. That is a clear straw man fallacy.
  We never claimed that. On the contratry. We said the gas usage would be 15M or more.

• Then, as we also said, using the model assuming 15M for every block is a minorant. At a starting price of 51 Gwei for example, this shows that in 23h an attacker would have to spend at least 104M.

• As we said, at some points in the attack, he must spend more. Because, looking at the mempool, he will see that he needs to send transactions with more than 15M.

Thereby, our model is conservative. Even so, it allows for a safe reduction of the 7 day challenging period, because it is not profitable to make a DoS attack to send invalid batches and then defending them on L1.

This is not hard to understand, and we kindly ask you to not put false words in our mouths.
I am sorry, but read carefully and then answer us properly with clear and meaningful topics.

Regards,
3s_drep_fi and @daniFi

[edfelten]

Earlier in the thread you claimed this:

Therefore, if exponential evolution were to occur, it would be short-lived, and block builders would quickly fill blocks of only 15 million to maximize their rewards and encourage transaction participation, as higher fees would be too expensive for users. So, in reality, the DoS attack will be done with blocks filled around 15 million, because that is where the economic competition really is.

I have been arguing that that claim of yours is not correct, by showing that validators do in fact fill blocks to more than 15M gas, and this happens very frequently.

The fact is that validators are willing to build blocks beyond 15M gas. That being the case, if an attacker tries to fill all blocks, the result will be an exponential increase in the basefee, so the cost of the attack will increase exponentially.

The reason for this is also clear. No rational validator would leave space in a block they are proposing, when they can earn more by filling that space.

This is an important design feature of the Ethereum gas pricing market: it responds to transaction flooding attacks (i.e. attacks that try to fill blocks in order to crowd out normal traffic) by escalating the price exponentially, and the escalation continues until the attacker stops the attack.

[tiago090499]

Due to a lack of transactions in the mempool and other factors, blocks in contemporary Ethereum are not filled to their maximum of 30 million gas.

During a denial-of-service attack, it is reasonable to assume that the attacker must ensure that the blocks are completely full in order to exclude other transactions, since a rational block builder would always add an extra transaction, resulting in higher fees.
This means an attacker must spend 30 million gas to initiate a DOS attack. However, the base fees will increase exponentially, which is a crucial point.

Assuming the user conducting the fraud-proof is also a rational user and is not conducting it out of love for the blockchain but for the reward he will receive, he will only post a fraud-proof on the blockchain if its net profit is positive. I mean “reward minus fees”.

This signifies that as soon as the base fees exceed the reward (which occurs quite quickly due to the exponential growth of the base fees), the malicious operator performing the DOS is no longer required to fill the block. To maintain the base fees at a level at which no fraud proofs will ever be issued, he need only maintain the block size at 15M.

This would be the rationale for assuming that the block space will remain at 50% capacity even though the blocks were initially filled to capacity.

[tiago090499]

In reality, the block space will fluctuate around 15M gas, as additional transactions (excluding fraud-proof) may continue to be posted to the blockchain, meaning that the base fee may continue to increase over time, albeit not exponentially. This also results in the malicious operator not needing to fill as much as 15M gas, as base fees may decrease as long as they do not fall below a threshold where issuing a fraud-proof becomes economically rational.
This behaviour is hard to predict, and since the amount of gas consumed by the operator will fluctuate around 15M, it can be assumed that the amount of gas consumed is constant and equal to 15M.

[daniFi]

Dear @tiago090499,

Exactly, this is precisely the rationale behind the model. Therefore, it is important to address this circumstance as a plausible attack and find ways to avoid it, which is our ultimate effort with the series we published. It is important to note that, in our model, the GasUsage variable can be any value from 0 to 30M. However, in a DoS scenario, we used 15M as the bare minimum, which is also the more plausible outcome.

Kind regards,
daniFi and @3s_drep_fi